Penyebaran Dua Jenis Fluida Menggunakan CFD

Program CFD mempunyai peranan yang penting dalam membantu menyelesaikan berbagai permasalah di bidang fluida. sebelumnya telah kita ketahui CFD dapat membantu kita mensimulasikan penyebaran temperatur di dalam suatu ruangan, pola aliran udara, perpindahan panas dan masih banyak lagi. kali ini kita akan belajar bagaimana mensimulasikan penyebaran dua jenis fluida yang berada di dalam suatu ruangan. Kondisi kasus yang akan di ambil adalah sebagai berikut:

•  sebuah ruangan yang vacum diberikan dua buah inlet dan satu outlet, inlet satu berada di bagian kiri atas dimasukan udara dengan kecepatan 0,01 m/s sedangkan inlet 2 berada di bagian kiri bawah ruangan dimasukan CO2 dengan kecepatan 0,1 m/s.
• kondisi inlet 1 lebih besar dibandingkan dengan inlet dua sehingga meskipun kecepatan udara yang masuk melalui inlet 1 lebih keci, namun jumlah udara yang masuk lebih banyak.
• outlet hanya berjumlah satu buah sebagai tempat keluarnya udara dan CO2 dari ruangan. kondisi ruangan 2 dimensinya adalah sebagai berikut:

  

setelah grid di bangun, maka untuk mengaktifkan dua jenis fluida kita menggunakan metode spesies (aktifkan species dengan cara):

kemudian masuk ke input-> atur spesies, buat spesies 1 udara dan species 2 CO2

atur kecepatan pada bagian inlet 1 dan inlet 2 pada bagian: input-> KS lalu masukan kecepatan udara dan CO2 masing masing  0,01 dan 0,1 m/s.

 setelah semua kondisi di atas diberikan, maka langkah selanjutnya adalah iterasi model hingga konvergen. sehingga dapat dilihat hasil dari penyebarannya seperti di bawah ini

• penyebaran fraksi massa

•  penyebaran fraksi mol

            

dari hasil simulasi di atas terlihat penyebaran udara di dalam ruangan, pada bagian atas udaranya lebih banyak karena langsung berhubungan dengan saluran inlet. sedangkan pada bagian bawah kiri hampir tidak ada konsentrasi udaranya dikarenakan pada kondisi bersamaan juga dimasukan CO2. pada bagian tengah ke arah kanan konsentrasi keduanya cenderung rata dikarenakan sudah jauh dari inlet 1 dan inlet 2.

Beban Kalor Kamar

       seperti sudah dijelaskan pada postingan sebelumnya ada beberapa komponen yang membuat kamar terasa panas dan  udara didalamnya susah bersirkulasi dengna baik seperti kalor dari dinding, alat elektronik, dari penghuni dan dari ventilasi dan atap. berikut adalah dasar teori awal besaran beban kalor yang diterima oleh kamar.

1.         Beban kalor pada dinding

-          Dinding sebelah utara, selatan dan barat memiliki koofigurasi yang sama sehingga beban kalor untuk masing-masing dinding adalah:

Luas dinding(3 x 3 meter)            = 9 m²

Tebal dinding                                    = 0,12 m

Material tembok batu bata ditambah plesteran dari sisi luar dan dalam. Sehingga nilai beban kalornya

q = UA CLTD_cor

CLTD_cor = CLTD_table + (78 – t_in) + [(t_o – DR/2)-85]

dimana:

U           = 1/R_total

R            = hambatan panas (bergantung pada material)

A            = Luas penampang dinding

CLTD     = Cooling Load Temperature Different

-          Tembok bagian timur

Luas dinding(3 x 3 meter)             = 9 m² – ( 0.66 m² + 0,64m² + 2 m²)

                                                    = 5,7 m²

Tebal dinding                                = 0,12 m

Material tembok batu bata ditambah plesteran dari sisi luar dan dalam. Sehingga nilai beban kalornya

q = UA CLTD_cor

CLTD_cor = CLTD_table + (78 – t_in) + [(t_o – DR/2)-85]

2.         Beban Kalor dari Pintu dan Jendela

Q = SC x SCL x A_jendela

Dimana :      SC                = SHGF / 0.87 ,

SHGF            = Solar Heat Gain Factor

                        SCL         = Solar Cooling Load

                        A              = Luas penampang tembok

Luas penampang jendela = 0.66 m²

Tipe jendela: awning

SHGF jendela terbuat dari kaca = 0.63

3.      Beban Kalor akibat ventilasi udara

Q _sensible = 1.08 x Q x (T₀ – T_i )

Q_latent = 4.680 x Q x W_oi

4.    Beban kalor karena manusia

Penghuni kamar berjumlah 1 orang yaitu penulis sendiri sehingga besarnya beban kalor yang ditanggung adalah sebesar

Q _sensible = q_s / person x CLF x N people

Dimana :      CLF = Cooling Load Factor

                        q_s = kalor sensible yang dihasilkan setiap orang

                        N = jumlah orang                            

Q_latent = q_L / person x N people

Dimana :     

q_L            = kalor latent yang dihasilkan setiap orang

N             = jumlah orang

5.      beban kalor akibat peralatan elektronik

Setiap peralatan elektronik yang adal di kamar akan memancarkan kalor sensible dengan persamaan:

q_s = 3.412 Btu/ W.h x CLF x Ws

Dimana :      CLF = Cooling Load Factor

                        Ws = Heat gain rates for equipment

sumber " buku ASHRAE"

Sinopsis Analisa Aliran Dalam Kamar

Latar Belakang

Kamar tidur merupakan tempat yang banyak dipakai oleh manusia untuk menghabiskan waktu di malam hari. Untuk sebagian orang terutama pelajar kenyamanan ruang kamar sangat penting  guna menunjang kinerja belajar. Sistem ventilasi yang buruk yang kebanyakan dimiliki oleh kamar kosan seringkali membuat mahasiswa tidak nyaman dan merasa panas ketika berada di dalam kamar kos dan membuatnya harus membuka pintu kamar agar udara luar masuk. Tentu hal ini sedikit mengganggu karena harus membuka pintu terlebih dahulu untuk mendapatkan udara segar. Cara lain yang biasa dilakukan adalah menghidupkan kipas angin.

Perlu dicermati, pemakaian kipas angin untuk mendinginkan ruangan tidaklah efektif. Hal ini dikarenakan kipas angin biasa hanya bekerja dengan memutar udara di sekitarnya dan  tidak dapat mengusir panas dari dalam ruangan. Jadi, yang dikerjakan oleh jenis konvensional itu hanya memutar udara di sekitarnya.

Untuk mengusir panas di ruangan yang langsung berhubungan dengan udara luar pemakaian exhaust fan lebih efektif dibanding dengan kipas angin dan udara di dalam ruang kamar akan lebih sejuk dan bersih. Hal ini dikarenakan  exhaust fan itu mengeluarkan udara panas yang ada di dalam ruangan dan membawa masuk udara sejuk ke dalam ruangan,

Tujuan

Pada tugas kali ini penulis berusaha untuk menganalisis kondisi aliran udara di kamar kosan dengan menggunakan exhaust fan dan tanpa exhaust fan. Selain itu, dilakukan juga perhitungan beban kalor dalam ruang kamar. Perhitungan beban kalor akan menggunakan beberapa metode numerik seperti metode iterasi dan least square  yang kemudian akan dibuat program komputasi untuk memudahkan proses perhitungan beban panas dan kebutuhan exhaust fan dan pengaruhnya terhadap aliran dan kondisi udara di dalam kamar.

Kondisi Ruang Kamar

Kamar yang dijadikan objek penelitian adalah kamar kos dengan dimensi 3 x 3 x 3 m.  Dinding sebelah barat, selatan dan utara tidak terkena sinar matahari karena langsung berbatasan dengan dinding kamar sebelah.  Sinar matahari mengenai bagian atap dan setengah dinding sebelah timur.  Konfigurasi kamar dapat dilihat pada gambar di bawah ini:

Dimensi komponen kamar :

      1.       Ruang kamar      = 3 x 3 x 3

      2.       Pintu kamar        = 1 x 2 meter

      3.       Pintu toilet          = 0,7 x 2 meter

      4.       Toilet                 = 1 x 1,3 meter

      5.       Jendela              = 0,6 x 1,1 meter 

      6.       Tempat tidur      = 2,4 x 1,2 meter

      7.       Lemari buku      = 0,3 x 0,4 meter

      8.       Meja belajar      = 1 x 0,5 meter

      9.       Lemari pakaian  = 1,1 x 0,5 meter

      10.   Rak                   = 0,25 x 0,4 meter

Sumber panas yang ada di kamar antara lain

a.       Lampu  LED 23 watt                 1 buah

b.      Lampu LED 18 watt                  1 buah

c.       Laptop 40 watt                          1 buah

d.      Manusia                                     1 orang

e.      Dinding                                       4 sisi

f.        Atap kamar

 

Algoritma penelitian

Untuk melakukan penelitian ini beberapa langkah dan pendekatan yang dilakukan dapat dilihat pada algoritma di bawah ini:

      a.       Mengukur geometri kamar

      b.      Mengelist properti dan furniture kamar

      c.       Hipotesis awal mengenai baban kalor dalam kamar, dinding, alat alektronik, dan penghuni

      d.      Mencari literatur mengenai beban kalor pada bangunan

      e.      Perhitungan beban kalor

      f .        Analisa

      g.       Kesimpulan

Aliran Unsteady Stead

Jika pada kasus-kasus sebelumnya kita menganalisa aliran tanap memasukan parameter waktu. pada kasus ini simulasi aliran unsteady. aliran unsteady adalah kondisi pola  aliran yang mengalami perubahan seiring dengan berubahnya waktu. sebagai contoh adalah ketika sebuah tangki air dibuka kerannya. lama kelamaan alirn keran akan melambat seiring dengan berkurangnya air di dalam tangki. 

karena memasukan parameter waktu, maka persamaan matematis untuk aliran unsteady flow lebih kompleks dibandingkan dengan steady flow. untuk menyederhanakan kasus, biasanya interval waktu harus diberikan dalam perhitungan maupun simulasi sehingag hasil perhitungan diferensiasi dan integral bisa akurat.

untuk membuktikan kasus unstedy flow, maka dilakukan simulasi terhadap perpindahan panas antara pada plat yang memiliki perbedaan temperatur sepanjang platnya.  kondisi nya seperti pada gambar dibawah ini:

langkah-langkah memulai simulasinya adalah sebagai berikut:

1. buat geometri platnya dengan : input-> domain (tentukan ukuran plat) pada kasus kali ini ukuranya adalah panjang 1 meter dan tinggi 0,1 meter dengan cell arah I 10 dan jumlah cell arah J 3. 

         

1. s
2. tentukan atur kondisi Wall 1, Wall 2, dan Wall 3 dengan cara: input->  cell atur seperti gambar dibawah ini

           
     3. atur  model simulasi dengan memasukan parameter waktu, perpindahan panas konduksi dan lain lain
         gambar di bawah ini:
 

        

        4. tentukan kondisi sempadan pada wall 1( flux panas = 0), wall 2 (temperatur 273 K) seangkan pada
            wall 3 nilai kondultifitas termalnya 10 w/mk
        5. untuk mengatur kondisi di wall 3 pada 473, dibutuhkan metode "tempel". metode ini dibutuhkan   
            agar wall 3 tidak terbaca 273 K. berikut cara menentukanya:

           

       dari kondisi yang telah dibuat  maka setelah dilakukan iterasi hasil simulasi sebagai berikut:

    1.  pada detik ke 1

     2.   pada detik ke 300

     3.  pada detik ke 500

       
      4.  pada detik ke 1000

   

  dari hasil simulasi di atas terlihat bahwa semakin lama maka kondisi plat dari kanan ke kiri akan semakin dingin. hal ini dikarenakan kondisi flux panas dari wall 1 kita kondisikan 0. jika simulasi diteruskan maka lama kelamaan kondisi plat akan 273 semua.



  

Jawaban UTS Komputasi Teknik

1.  Secara numerik tentukan fungsi profil kecepatan aliran laminar pada setiap jarak X dari ujung pelat bagian depan (aliran hulu). Bandingkan dengan hasil analitis. Jelaskan jawaban saudara

2.  Untuk Soal no 1. Tentukan, secara numerik, hambatan pelat tersebut. Bandingkan dengan hasil analitis.     

3.  Jika bagian bawah pelat (soal no 1) diberikan fluks panas, tentukan, secara numerik, fungsi profil 

    temperatur  pada lapisan batas termal. Bandingkan dengan hasil analitis.

4.  Tentukan , secara numerik, koefisien perpindahan panas konveksi untuk soal no. 3. Bandingkan dengan hasil analitis. 

jawaban dari pertanyaan di atas adalah:

1.  Aliran kecepatan laminar yang mlewati plat datar dan tipis dilakukan dengan langkah-langkah di bawah ini:

- menentukan panjang dan tipis plat yang akan dilewati aliran. Untuk kasus ini panjang plat yang dilewati 1 meter dan tebal plat 0,1 meter. 

     - menentukan posisi udara masuk(inlet 1) dan inlet 2

     - menentukan kecepatan udara yang masuk ke pangkal plat.

- tekanan di inlet 2 dianggap vacum sehingga yang mempengaruhi profil kecepatan hanya  dari plat saja.

Profil aliran laminar yang melewati plat berdasarkan reynold number yaitu

Re = ρu₀L/ μ

Dan berdasarkan teori adalah: 

 

Pada simulasi yang dilakukan, jumlah cell yang digunakan adalah 80 pada arah i dan 40 pada arah J.  Setelah dilakukan simulasi dengan kecepatan inlet 1 0,1 m/s hasil profil kecepatanya didapat sebagai berikut :

 

     Dari hasil yang didapat sesuai dengan teori yang ada dimana pada bagian awal aliran akan mengalami  developed dan semakin kearah ujung aliran akan fully developed. Nilai kecepatan untuk beberapa node ditampilkan sebagai berikut:

 

 

Hasil simulasi dari kontour kecepatan pada aliran laminar tersebut terlihat pada grafik di bawah ini.  Node yang diplot hanya 4 node yaitu 18, 22, 25 dan 30. Dari grafik terlihat bahwa semakin ke arah kanan grafik semakin besar artinya aliran semakin fully developed.

 

2.  hambatan

    

Nilai shear stress pada plat akan mempengaruhi aliran. Semakin laminar aliran , nilai shear stress akan semakin besar, sebaliknya nilai shear stress pada aliran turbulence akan semakin kecil. Seharusnya pada simulasi semakin ke arah ujung profil shear stress yang dialami akan semakin kecil. Persamaan shear stress  seperti di bawah ini.

.τ = μ (du/d y)

    Seteah di simulasi maka hasilnya sebagai berikut:

 

Dari gambar di atas terlihat, shear stress pada bagian awal labih besar dibandingkan dengan pada bagian ujung dikarenakan pada bagian ujung aliran sudah mengalami fully develope.

•      Program VB gauss jordan untuk mencari persamaan soal no 1 dan 2 adalah:

Private Sub CommandButton1_Click()

Dim A As Double

    Dim b, c, d, e, f, a0, b0, c3, c4, c5, j3, j4, j5 As Double

    For i = 1 To 50

        A = A + Cells(1 + i, 10) ' jumlah total x

        b = b + Cells(1 + i, 11) ' jumlah total y

        c = Cells(1 + i, 10) ^ 2 ' menulis pangkat

        Cells(1 + i, 12) = c

        d = d + Cells(1 + i, 12) ' jumlah x2

       

        c3 = Cells(1 + i, 10) ^ 3 ' menulis pangkat 3

        Cells(1 + i, 13) = c3

        j3 = j3 + Cells(1 + i, 13) ' jumlah pangkat 3

                c4 = Cells(1 + i, 10) ^ 4 ' menulis pangkat 4

        Cells(1 + i, 14) = c4

        j4 = j4 + Cells(1 + i, 14)

               

        e = Cells(1 + i, 10) * Cells(1 + i, 11) ' x kali y

        Cells(1 + i, 15) = e    ' menuliskan nilai x*y

        f = f + Cells(1 + i, 15) ' jumlah xy

       

        c5 = (Cells(1 + i, 10) ^ 2) * Cells(1 + i, 11) ' x*y

        Cells(1 + i, 16) = c5

        j5 = j5 + Cells(1 + i, 16) ' jumlah x2y

       

    Next

        Cells(55, 10) = A

        Cells(55, 11) = b

        Cells(55, 12) = d

        Cells(55, 13) = j3

        Cells(55, 14) = j4

        Cells(55, 15) = f

        Cells(55, 16) = j5

               ' Cells(9, 5) = f

        'denom = (7 * d) - (a * a)

        'a0 = ((b * d) - (a * f)) / denom

        'b0 = ((7 * f) - (a * b)) / denom

        ' Cells(3, 10) = "y=" & b0 & "x" & "+" & a0

End Sub

   Dari program tersebut kemudian akan di dapat A , b dan c. Kemudian nilai tersebut dapat dijadikan matrik untuk tiap node. Selanjutnya akan didapatkan hasil  least squarenya

3.

Jika plat diberikan heat flux, maka temperatur di dekat plat akan semakin panas sehingga akan mempengaruhi pola aliran.  Penyebaran heat flux dan temperaturnya dapat dilihat dengan menggunakan persamaan:

q” = - k (∂T/∂y) ]_y=0

(∂T/∂y) = (T_o – T₁)/ (y_o-y₁)

Dimana:

T_o         = temperatur plat

T₁         = temperatur yang diberikan pada

Y_o        = 0

Y₁        = kondisi pada y sama dengan i

Langkah-langkah melakukan simulasinya adalah:

-          Tentukan To yang ingin diberikan pada plat.

-          Tentukan kecepatan awal Uo sesuai dengan soal nomor 1.

-          Tentukan besaran heat flux pada plat.

-      Dengan melakukan simulasi maka akan didapatkan nilai penyebaran temperatur dan panasnya pada setiap node.

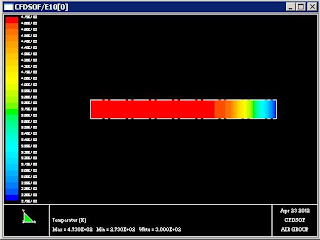
Dari hasil simulasi yang dilakukan maka hasilnya adalah:

 

•     temperatur 

 

•          Heat flux 

 

•      Kecepatan

Berdasarkan simulasi yang telah dilakukan dapat dilihat bahwa:

a.       Pola kecepatan sama dengan kasus sebelum diberi heat flux dimana pada bagian awal aliran akan mengalami  developed dan semakin kearah ujung aliran akan fully developed.

b.      Heat flux hanya terlihat pada plat dan  sedikit di atas  plat. Hal ini dikarenakan perpindahan panasnya belum diberikan perbedaan temperatur dari udara luar.

c.       Temperatur semakin besar ke arah ujung dikarenakan temperatur panas pada bagian awal plat ditiup oleh aliran. Sehingga temperatur semakin ke ujung akan semakin tinggi.

4.  

 

Koefisien pindah panas didapatkan dari persamaan di bawah ini:

hx = 0.04 k/x (Re^0.9)(Pr^0,333)

Dimana:

                hx           = koefisien perpindahan panas pada arah x

                k               = konduktivitas termal.

                Re _x             = reynold number pada arah x

                Pr            = prandtl number pada arah x

    Langkah simulasinya sama seperti nomor tiga. Hanya saja setelah untuk membuktikanya diperlukan perhitungan berdsarkan persamaan di atas. Hasil simulasinya adalah sebagai berikut: